Aerospace Structures

Intro to Structural Analysis

Content Tags: Hookes Law, Internal Loads, Strain, Stress, Supports Created: March 6, 2022 9:10 AM

Stress

• Stress on a small element of a material under load
• 2 types of stresses:
  • Normal
  • Shear
• Ask what does a load do to a cross section?
  • What loads are there? Moments? Stresses?

Shear and Normal stress produce fundamentally different forces in the material

• Normal is a compressive or stretching action
• Shear is considered as though it acts on a plane

What is strain? What are the units of strain?

• Strain is a change in material distortion under the effect of a stress
• The units are dimensionless (Change in Length/Length)

What is normal strain? What is shear strain?

• Normal strain acts through the cross section of the body to lengthen or contract it
• Shear strain creates torsion and warping

What is a positive and negative normal strain?

• Positive normal acts in torsion
• Negative acts to compress

What is a positive and negative shear strain?

• Positive and negative only alters the direction of the torsion. So clockwise or counter-clockwise

Normal Strain is?

• The slope of displacement

Shear Strain is?

• Still non-dimensional
• Relationship??

Poisson’s ratio?

• Ratio of strains. Reaction strain acting in orthogonal direction is cause by original strain.

Hooke’s Law?

• Constant Value = Stress/Strain, while elastic.

Plane (2D) Problems

• Disregard a particular aspect because nothing important is happening in the other access out of plane. This needs to be carefully evaluated.

Beams and Plates

• Take a beam and extrude it for plates
• Plates have a poisson effect that beams don’t have

2D State of Stress

• Your stresses are dependant on your coordinate system
• Can resolve state of stress into principal stress
• Use Moores circle
• A cylinder under normal tension will fracture vertically
• A cylinder under shear will fracture diagonally. Imagine the shear diagram deforming a square into a kite shape.

Aircraft Materials

• Common Materials:
  • Metals (Most discussed)
  • composites
  • Sandwich

Static Equivalence

• Same forces and same moments
• Internal loads must be equivalent to the external load that is acting on the body.
• Internal reaction loads are equal and opposite. The internal loads are not.

Partial Derivative

• The partial derivative is the derivative of a function with respect to one variable only
• This gives the rate of change, or slope, of a function with respect to one variable

Support Conditions

• Import drawings for supports. (Roller, Fixed, Pin). Add degree of freedom info.
• Rollers always provide a force in the Y direction regardless of the sign of the force. Not in the X direction. Or vice versa depending on the unit system.

Internal Loads

• 4 Types of internal loads:
  • Normal (N)
  • Shear (V)
  • Torsional (T)
  • Bending (M)

Force and Moment Diagrams

• Take a slice and determine the shear force and moment at that point (This is important for this course)

Reference Material

(1A)_Intro_to_structural_analysis-1.pdf

---

Euler Buckling

Created: April 28, 2022 11:02 AM

Euler Column Theory

• Valid, within the limits of assumptions
• Based on a perfect stable section column
  • The column is perfectly straight
  • Load is applied at the section centroid
  • Column material is homogenous
  • Stresses are in the elastic range
  • No local section instabilities (no twist or deformation)

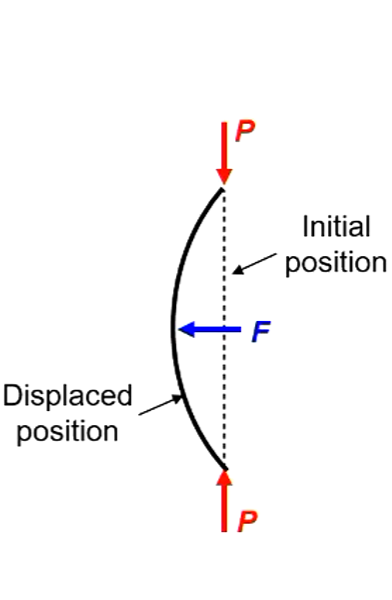
• Perfect column under compressive load P
• Load associated with buckling is $P_{CR}$
• If column is displaced by lateral load F

Derivation of Euler Buckling Equation

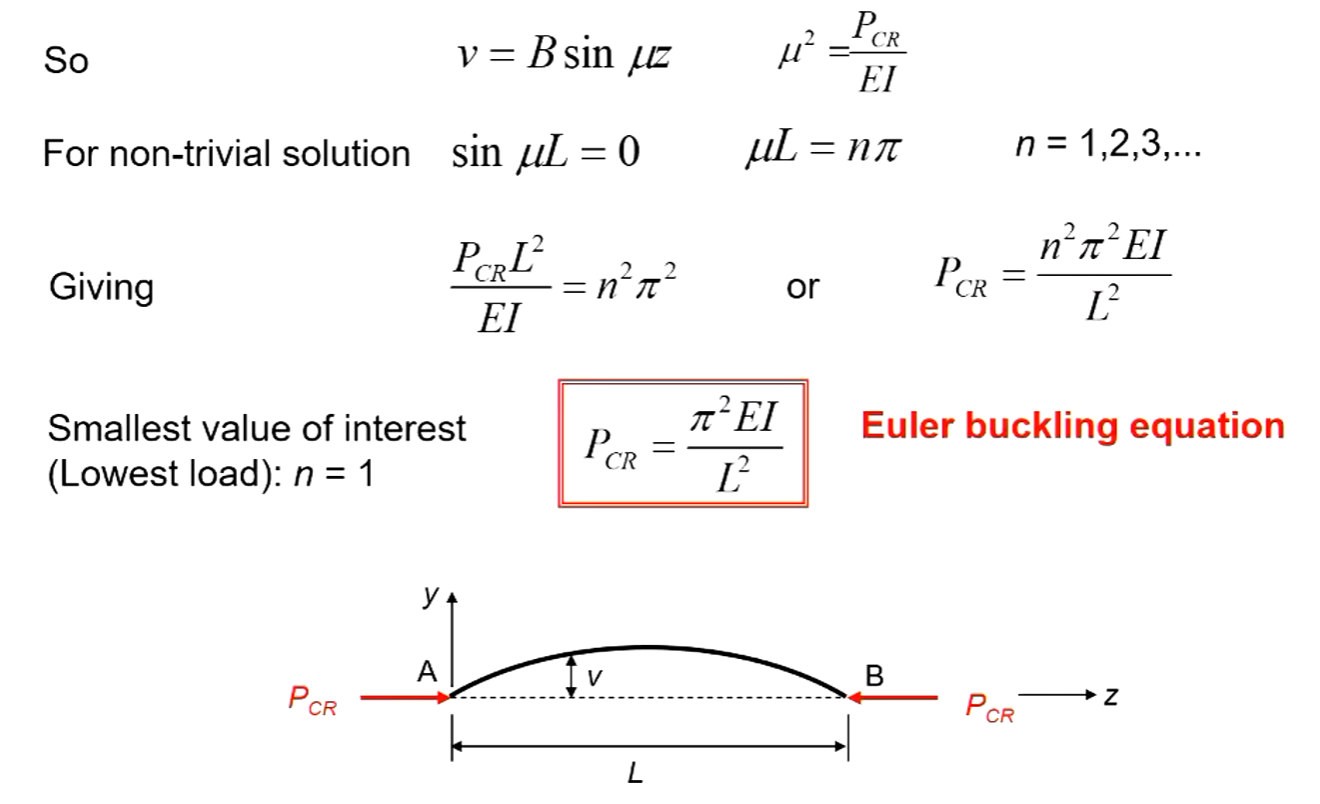
Buckling Modes

• Each n buckling mode (displacement shape) has an associated buckling load
• n = number of “half waves” in buckling mode shape

\[P_{CR} = {n^2\pi^2EI\over L^2}\]

Effective Length

End Fixity

• How the ends of the columns are restrained
• Most columns have some form of restraint (end fixity)
• To account for this, the effective length L’ is adopted $P_{CR} = {\pi^2EI\over (L’)^2}$

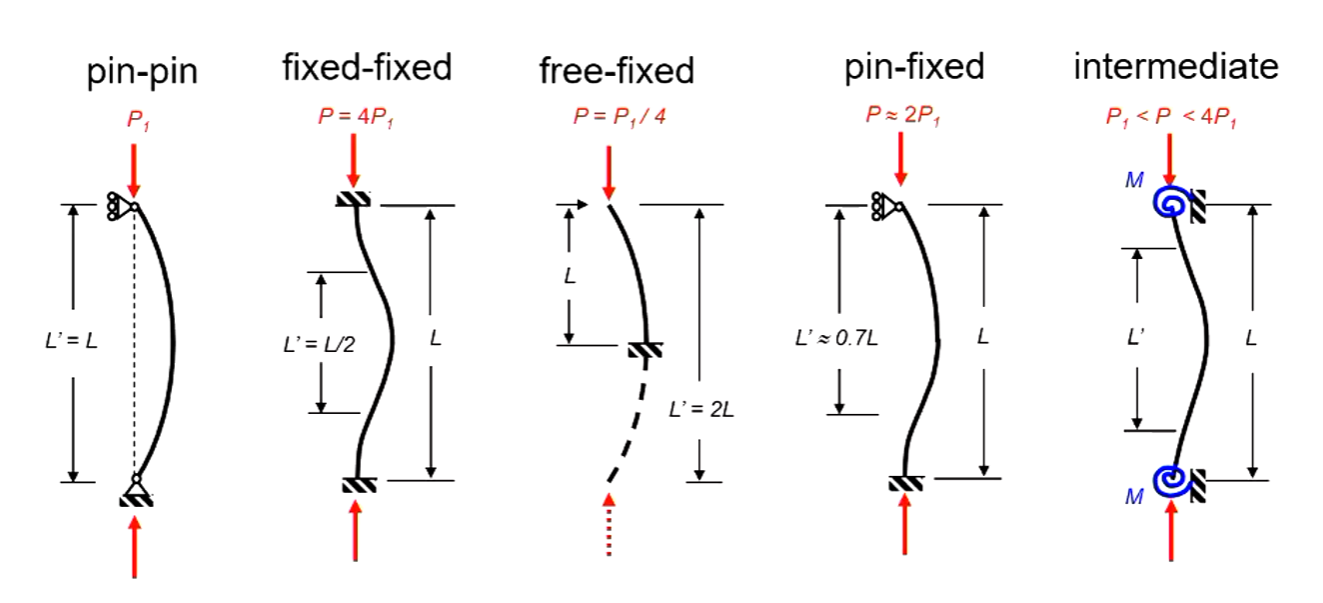
Second Moment of Area

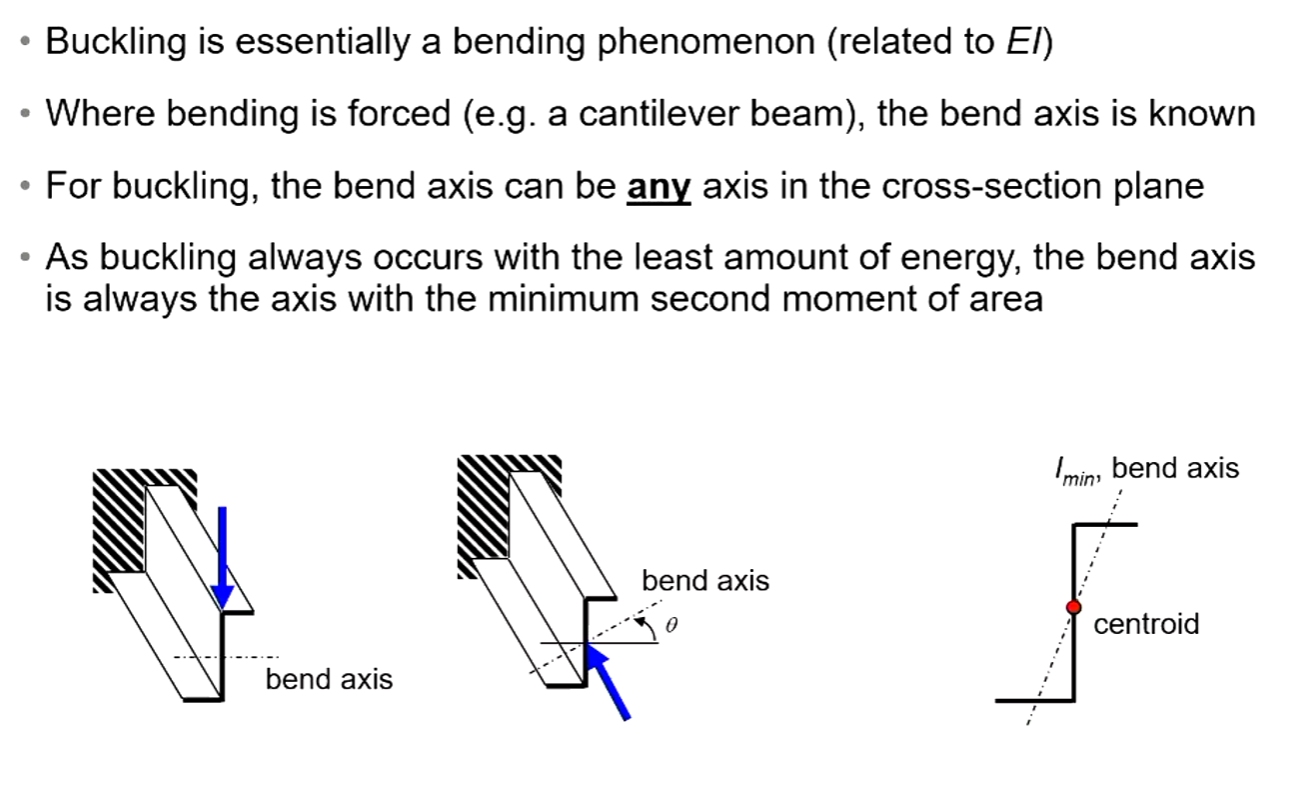
• Buckling always occurs around the axis of $I_{min}$

Stress Form of Buckling Equation

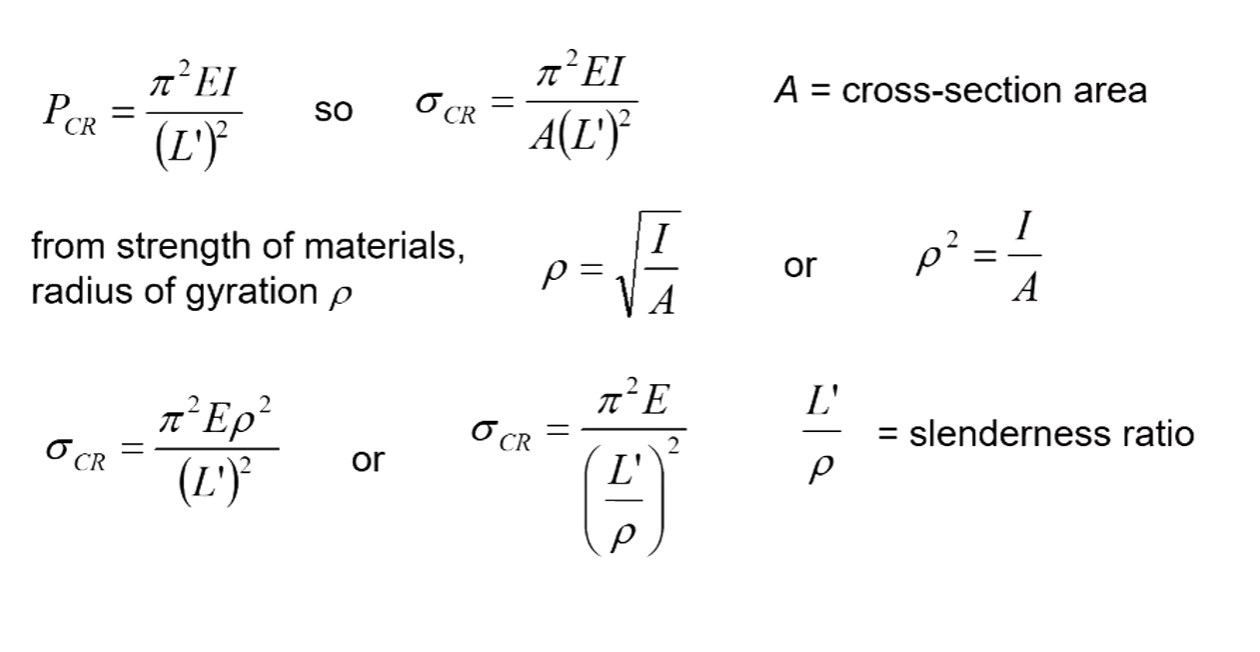
Column Curve

Inelastic Buckling

Column Curve Ranges

• Metal material behaviour is non-linear following yield or elastic limit
• “Long” columns buckle when material is still in elastic region
• “Short” columns undergo plasticity before buckling
• Euler theory will over-estimate the buckling stress in the case of a “short” column
• Very short columns (L’/$\rho$ ~ 10) fail by crushing, or “block compression”

Empirical Short Column Equations

• Empirical (test-based) relationships developed for buckling of thin-walled sections (which incorporates local buckling)
• Column curve is a structural response (not material)
• Empirical relationships developed for common sections and materials
• Linear and parabolic forms most common, other indices are possible.
• Linear:

\[\sigma_{CR} = \sigma_{c0} - k(L'/\rho)\]

• Parabolic:

\[\sigma_{CR} = \sigma_{c0} - k(L'/\rho)^2\]

• Stress $\sigma_{c0}$ is a property of the cross-section (assumed independent of length), and material
• Can be found using several approaches
  • Assumed equal to ultimate compressive strength $\sigma_{cu}$
  • Taken from test data for a very short column
  • Determined analytically or semi-empirically
  • Found using data sheets (e.g. ESDU), standards (e.g. MIL-HDBK), etc

Euler-Johnson Equation

• A type of parabolic short column equation

\[\sigma_{CR} = \sigma_{c0}[1-{\sigma_{c0} \over 4 \pi^2E}\cdot({L' \over \rho})^2]\]

Inelastic Plate Buckling

• Elastic-plastic behaviour for metals affects buckling
  • Similar behaviour previously seen for columns
• Buckling can occur at stresses above elastic limit
• Less common as requires thick plates
• One approach (less common in industry) treats the plate as a column
  • Relate the plate to an equivalant column using:

\[({L' \over \rho}) = {\pi \over \sqrt{k}} \cdot ({b \over t})\]

• Then simply use the above inelastic equation depending on the situation (Linear, Parabolic, Euler-Johnson)

Plate and Local Buckling

Flexural Buckling

• Global Buckling
  • Primary instability mode of the entire column, or instability due to overall column bending
    • Characteristic length ~ distance between supports

Rectangular Plates in Shear

• Buckling in shear is determined from the same equation
  • Analytical derivation of buckling not considered here
• A rectangular plate in shear develops a series of closely space buckling waves at approximately 45 degrees
• The effect of boundary conditions and plate size is similar to that of a plate in compression.
• We use a different graph to obtain our K values but the process is the same from a calculation standpoint.
• In shear buckling the b in the equation is always the smaller dimension
• $\sigma_{cr} = {KE ({t \over b})^2}$

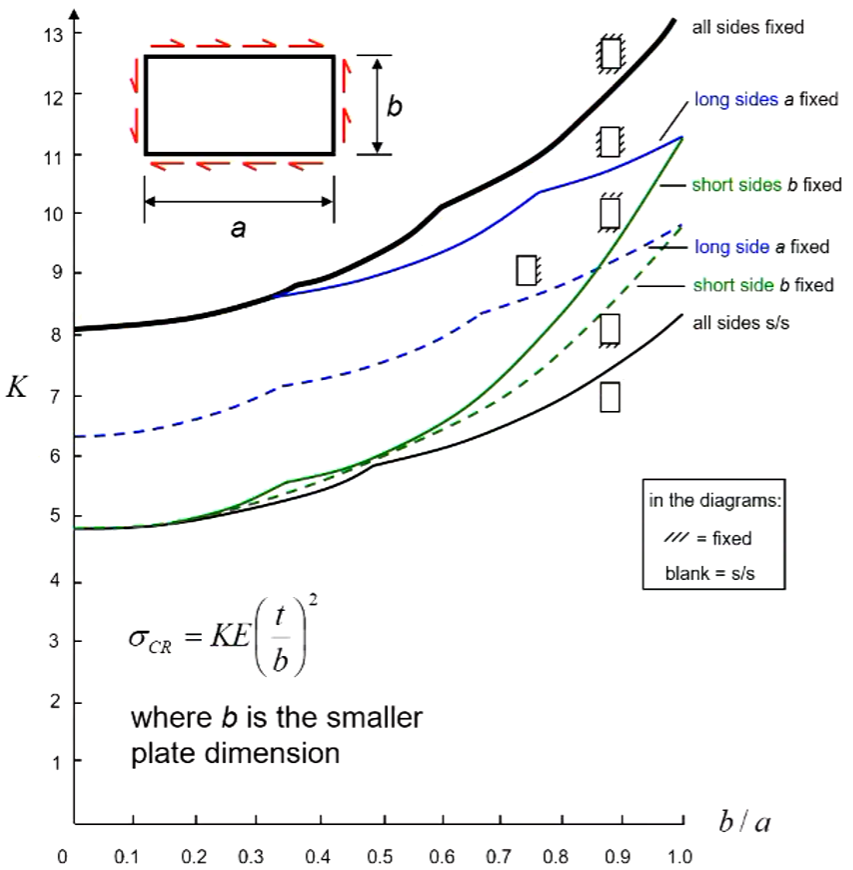
Rectangular Plates in Compression

• With plates we need to more carefully consider which mode of buckling will be take the least amount of energy.
  • Across the width of the plate mode 1 is still the lowest so only one half wave will be present
  • This is not true when considering the height.
  • The plates will buckle into a shape that is the closest to maintaining “square” buckles along its length. So each buckle will occur at lengths that approximate square sections of the total plate.

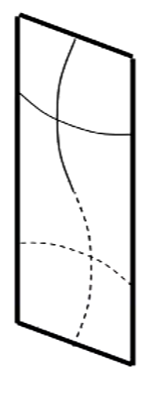
• As seen above the plate buckles into two “square” sections. This is the lowest energy buckling mode.
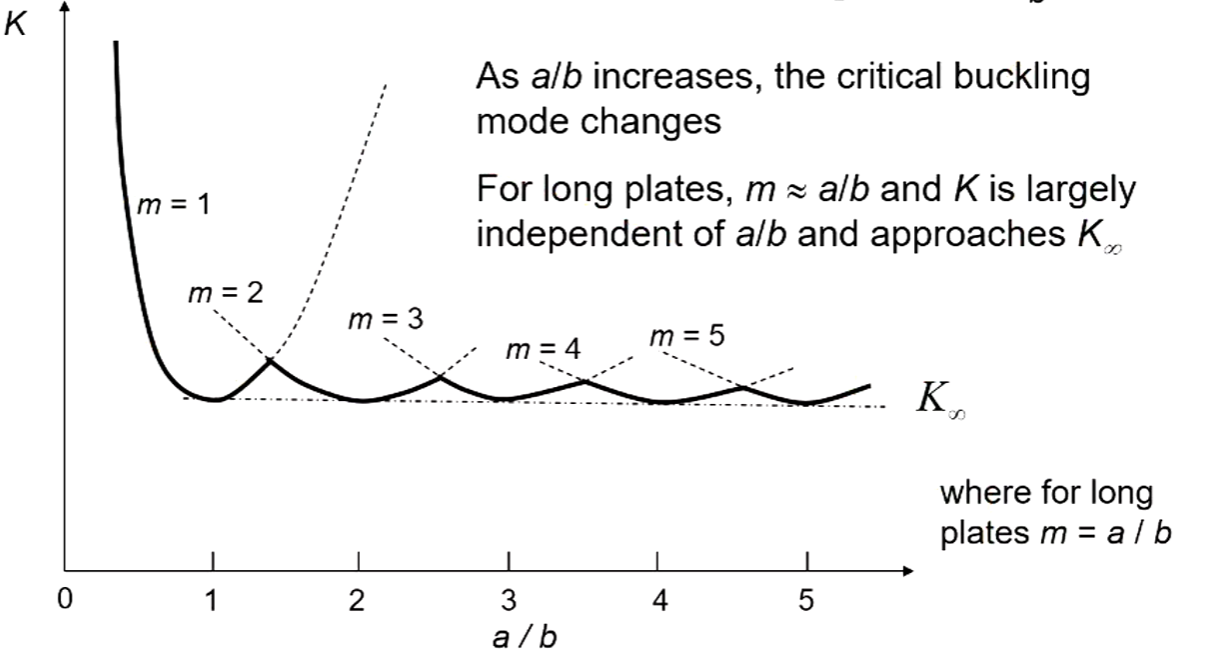
• $K_{\infty}$ is a good approximate for really skinny plates.

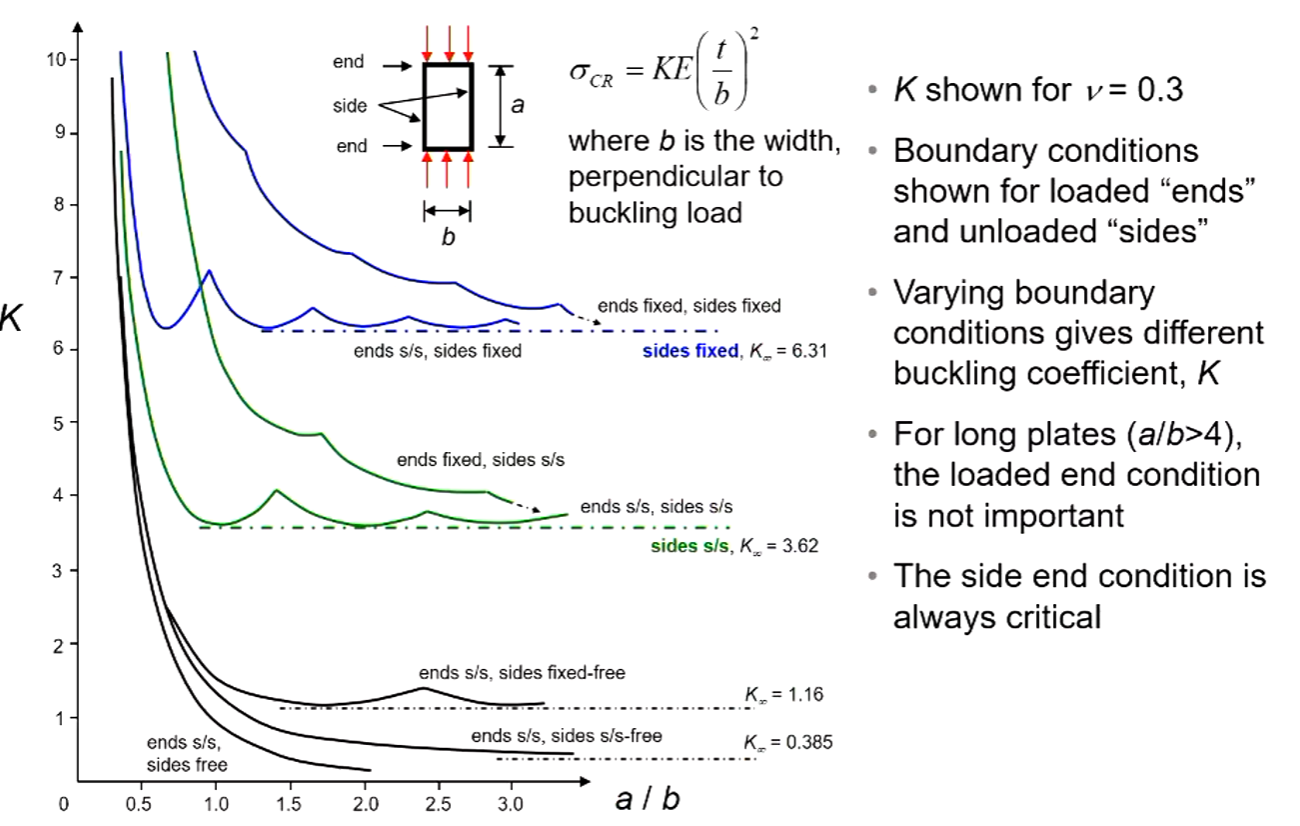
Plate Buckling Stress

• Compression and shear stresses on a plate can lead to buckling
• Buckling load of a flat plate is dependant on
  • Type of loading (compression, shear)
  • Material (E, v, t)
  • Edge support (fix, pin, etc)
  • Geometry of the plate (dimensions, aspect ratio)
• Buckling stress of plates is always:

\[\sigma_{cr} = {KE ({t \over b})^2}\]

Where,

• K is a buckling constant
  • Varies with restraint, geometry, loading, material
• E is elastic Modulus
• $({t\over b})$ is the ratio of the plate thickness to width.
• b is always the width of the loaded edge regardless of orientation for compression buckling

Local Buckling

• Occurs when the column acts like a collection of square plates. Common in thin-walled structures.
• Thin-wall panels can buckle before or after flexural buckling
• Usually confined to localised portions of the total length
  • Characteristic length ~ cross-section dimensions
  • Thin-wall columns see local buckling of the flanges
  • Stiffened beams see skins buckling between stiffeners
• Simple predictions for local buckling can be made by analysing the structure as a series of plates
• The corners of a cross-section and the stiffeners in a stiffened beam provide restraint
• Each segment or plate has different geometry and boundary conditions and requires separate calculation
• The restraint applied on each plate by the corners and stiffeners is difficult to determine
• In both cases the restraint should vary between a fixed and simple support
• Simple support can be assumed for conservative estimates unless the condition is known or given

Bending

Bending Stresses

• Bending of a beam causes compression and tension stresses on a cross-section (bending stresses)
• These are direct stresses, normal to the cross-section
• Between the compression and tension regions is a line of zero bending stesses, called the neutral axis
  • The neutral axis passes through the section centroids
  • The neutral axis has no deformation or stains associated with bending stress
• Bending of a beam can occur around two axes
  • The two in-plane axes of a cross-section
  • bend axes, moment, stress distribution, resists all change

Symmetric Bending

• Symmetric Bending occurs for bending of beams with one or two axes of symmetry
  • Axis of symmetry = “mirror plane”
• Bending behaviour is simplified as bending around the two axes acts independently
• Uses equation: $\sigma {bending} = {M{bending} \over I_x} y$
• For bending in two seperate axis we can calculate the stress for both and simply add them. Direct stress can also be added.

Asymmetric Bending Equation

• Bending always relates to a centroid coordinate system
• General equation for bending stress:

\[\sigma_z =({M_yI_x -M_xI_{xy}\over I_xI_y-I_{xy}^2})x +({M_xI_y -M_yI_{xy}\over I_xI_y-I_{xy}^2})y\]

Works for any bending problem. Including symmetric bending and single moment bending.

Bending Sign Convention

Thin Wall Assumptions

Equations

Equation	Explanation	Variables
$I_{x} = {bd^3\over 12}$	Second Moment of Inertia for a rectangle, measured from the x axis.	d is the direction perpendicular to the y axis.
$I_{x} = {b^3d\over 12}$	Second Moment of Inertia for a rectangle, measured from the y axis.	b is the direction perpendicular to the x axis.

Properties of Plane sections

• First Moment of Area (important for centroids)
• Second Moment of Area
• Rotation of Axes
• Parallel axis theorem

Stiffened Structures

• Consist of two structural elements, which can be assumed to perform seperate functions.

Shear

Shear flow

• Force on Length

\[q = {T \over 2A_E}\]

Where,

T = applied torque, Ae = area enclose by cross-section (mid-line)